细粉加工设备(20-400目)

我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。

MTW系列欧版磨粉机

稀油润滑系统，新型吊挂式笼式选粉机结构设计

LM立式辊磨机

采用新型碾磨装置自动化电控系统

5X系列欧版智能磨粉机

大型规模化环保智能磨粉机优选设备

LM矿渣立式磨

LM矿渣立式磨集破碎、干燥、粉磨、分级输送于一体

立式磨煤机

烘干与制粉二合一可边磨边烘干

雷蒙磨粉机

工业磨粉设备先驱，经济实用

更多了解

超细粉加工设备(400-3250目)

LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。

LUM超细立磨

LUM超细立磨结合现代磨粉理念

MW环辊微粉磨

采用新型碾磨装置自动化电控系统

粗粉加工设备(0-3MM)

兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。

LM砂粉立磨

大型效率与节能双高型砂粉制备产品

D是CA延长线上的一点

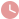
如图1所示，在Rt ABC中，∠C=90°，点D是线段CA延长线上

如图1所示，在Rt ABC中，∠C=90°，点D是线段CA延长线上一点，且AD=AB．点F是线段AB上一点，连接DF，以DF为斜边作等腰Rt DFE，连接EA，EA满足条件EA⊥AB．（1）如图，在Rt ABC中，∠ ACB=90°，AC=1，BC=7，点D是边CA延长线上的一点，AE⊥ BD，垂足为点E，AE的延长线交CA的平行线BF于点F，联结CE交AB于点G (3)当 BGE与 BAF相似时，求如图，在Rt ABC中，∠ ACB=90°，AC=1，BC=7，点D是边如图所示，在 ABC中，D是BC延长线上一点，CD=BC，E是CA延长线上一点，AE=2AC，若AD=BE，求证： ABC是直角三角形．答案分析由于告诉了AE=2AC，故延长AC至F，如图所示，在 ABC中，D是BC延长线上一点，CD=BC，E 点评本题主要考查了全等三角形的判定与性质，等腰三角形“三线合一”的性质，难度中等．由题目条件“AE=2AC”联想到中线倍长是解答本题的关键．练习册系列答案如图所示在 ABC中D是BC延长线上一点CD=BCE

如图1所示在Rt ABC中∠C=90°点D是线段CA延长线

（3）如图2，过D作DM⊥AE交AE的延长线于M根据余角的定义和三角形的内角和得到∠2=∠B，证得 ADM≌ BAC，由全等三角形的性质得到BC=AM，由于EF=DE，∠DEF=90°，推出∠4=∠5，证得 MED≌ AFE，根据全等三角形的性 2015年4月20日平行线的性质 > 试题详情难度：使用次数：138 更新时间：纠错 1 如图， ABC中，AB=AC，D是CA延长线上的一点，且∠B=∠DAM．求证：AM∥BC．查看答案如图， ABC中，AB=AC，D是CA延长线上的一点，且∠B 如图，在Rt ABC中，∠ACB=90°，AC=1，BC=7，点D是边CA延长线的一点，AE⊥BD，垂足为点E，AE的延长线交CA的平行线BF于点F，连结CE交AB于点G．（1）当点E是BD的中点时，如图在Rt ABC中∠ACB=90°AC=1BC=7点D是边CA延长 2014年12月29日已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且OA=AB=AD．（1）求证：BD是⊙O的切线；（2）解：（1）如图：连接OB，∵OA=AB=OB，∴ OAB是等边三角形，∴∠OAB=∠OBA=60°，∵AD=AB，∴∠ABD=∠D=12∠OA 百度首页已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上

如图，已知d是等边三角形abc的边ba延长线上的一点，过d作

2012年6月15日如图，已知d是等边三角形abc的边ba延长线上的一点，过d作de∥cb交ca的延长线于e，连接be、cd证明：（1）因为三角形ABC是等边三角形，所以角ABC=角ACB=60度，因为 DE//CB，已知：如图，D是 ABC的边BA延长线上一点，且AD=AB，E是边AC上一点，且DE=BC求证证明：过点D作BC的平行线交CA的延长线于点F，如图， C E D A B 8 F ∴∠C=∠F， ∵点A是BD的中点， ∴AD=AB，在 ADF和 ABC中， ∠C=∠F ∠DAF=∠BAC 已知：如图，D是 ABC的边BA延长线上一点，且AD=AB，E 2011年6月26日因为D在BC的延长线上由三角形外角和定理得：角ACD=角ABC+角A 所以角A=角ACD角ABC 同理：角ECD=角EBC+角E 所以角E=角ECD角EBC 又BE、CE分别为角ABC、角ACD的角平分线所以角EBC=1/2角ABC 角ECD=1/2角ACD 代入则有：角如图，D是BC延长线上一点，∠ABC和∠ACD的平分线交于E 2012年1月30日如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且AB=AD=AO ．（1）求证：BD是⊙O的切线；（2）若点E是劣弧BC上一点，AE与BC相交于点F，且∠ABE=105°，DB=2倍根号下3，求AE的长好心人帮帮忙展开我来答如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且

如图，在三角形ABC中，AB=AC，点E是CA延长线上的一点

2013年7月8日如图，在三角形ABC中，AB=AC，点E是CA延长线上的一点，点F在AB上，且角AEF=角AFE。求证：EF垂直BC 3 个回答 #合辑# 面试问优缺点怎么回答最加分？西尼艾尼 TA获得超过4708个赞知道小有建树答主回答量： 2921 采纳率： 36% 759万如图，在等腰直角\triangle ABC中，AB=AC，∠BAC=90°，点D是CA延长线上一点，点E是AB延长线上一点，且AD=BE，过点A作DE的垂线交DE于点F，交BC的延长线于点G(1)依题意补全图形；(2)当∠AED=α，请你用含α的式子表示∠AGC；(3)用等式表示线段CG与如图，在等腰直角 ABC中，AB＝AC，∠BAC＝90°，点D是如图，已知M是 ABC的边AB的中点，D是MC延长线上一点，满足∠ACM=∠BDM(1)求证：AC=BD；(2)若∠CMB=60°，求ABCD的值D CA MB 相关知识点：四边形平行四边形平行四边形基础平行四边形的判定如图，已知M是 ABC的边AB的中点，D是MC延长线上一点如图，三角形ABC中， E 是CA延长线上的点， D 是BA延长线上的点，AE=2 ，AD=3 ，EC=8，AB=7 ；如果三角形ABC的面积是21，请问：三角形ADE的百度试题结果1如图，三角形ABC中， E 是CA延长线上的点， D 是BA延长

[题目]已知:如图D是 ABC的边BA延长线上一点且AD＝ABE

【题目】下列说法正确的是 A “ 明天降雨的概率是 80%” 表示明天有 80% 的时间都在降雨 B “ 抛一枚硬币正面朝上的概率为 ” 表示每抛 2 次就有一次正面朝上 C “ 彩票中奖的概率为 1%” 表示买 100 张彩票肯定会中奖 D “ 抛一枚正方体骰子，朝上的点数为 2 的概率为 ” 表示随着抛掷次数的增 2016年12月2日已知：如图，在 ABC中，D是AC的中点,E是线段BC延长线上一点，过点A作BE的平行线与线段ED的延长线交点于点1∵AF∥CE∴∠ACE=∠ 已知：如图，在 ABC中，D是AC的中点,E是线段BC延长线上 2014年12月15日如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且A为DO中点，∠E=30°．求证：BD是⊙O的切线．展开我来答 1个回答 #热议# 应届生在签三方时要注意什么？诰雌壬1417 超过69用户采纳过TA的回答知道答主回答量： 128 采纳率：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且A 【例9】（2019春•鄂城区期末）如图，在 ABC中，∠C＝90°，E是CA延长线上一点，F是CB上一点，AE＝12，BF＝8，点P，Q，D分别是AF，BE，AB的中点，初中平行四边形的性质与判定是初中数学中的重要内容。平行四边形是指有两组对边分别平行的四边形。【例9】（2019春•鄂城区期末）如图，在 ABC中，∠C＝90

ABC是等边三角形，D是BA的延长线上的一点，E在BC上

2011年12月19日首先在BA上找一点F使得BF=AD ABC是等边三角形 ∴AB=AC=BC ∠B=∠BCA=∠BAC=60° ∵BF+FA=AB ∴FA+AD=DF=AB=CA 即DF=CA ∵DE=DC ∴∠DEC=∠DCE ∵∠DEC=∠B+∠FDE ∠DCE=∠BCA+∠ACD4已知正方形ABCD与正方形CEFG，M是AF的中点，连接DM，EM．（1）如图1，点E在CD上，点G在BC的延长线上，请判断DM，EM的数量关系与位置关系，并直接写出结论；（2）如图2，点E在DC的延长线上，点G在BC上，（1）中结论是否仍然成立？请2020中考数学几何探究专项训练(倒数第二大题) 百度文库(3分) (2019八下新洲期中) 如图,已知M是 ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDMD CA MB(1) 求证:AC=BD;(2) 若∠BMC=60°,求部的值答案参考答案(12分)如图,已知M是 ABC的边AB的中点,D是MC的延长线上 2013年2月14日（2012•德阳）如图，点D是 ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）．以BD、BF为邻边作平行四边形BDEF，又AP平行且等（2012•德阳）如图，点D是 ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B2012 德阳如图,点D是三角形ABC的边AB的延长线上一点,点

如图,在 ABC中,AB=AC,D为CA延长线上一点,DF⊥BC,,交AB

2013年10月13日如图,在 ABC中,AB=AC,D为CA延长线上一点,DF⊥BC,,交AB于点F求证∠d=∠AFD因为三角形中AB=AC，所以角B=角C；因为DF垂直BC，所以角FEC=90度=角FEB，因为对等关系，所以角BFE=角D；因为角BFE和角AFD是对角，所以角AFD如图1所示，在中，，点D是线段CA延长线上一点，且AD=AB，点F是线段AB上一点，连接DF，以DF为斜边作等腰，连接EA，EA满足条件（1）若，，BC=2，求AB的长度；（2）求证：AE=AF+BC；（3）如图2，点F是线段BA延长线上一点，探究AE、AF、BC 如图所示，在Rt ABC中，∠ C=90°，点D是线段CA延长线上 D CM PB N如图，分别以线段AB的两个端点为圆心，以大于\dfrac{1}{2}AB长为半径作弧，两弧交于点M和点N，在直线MN上取一点C，连接CA，CB，点D是线段AC的延长线上一点，且CD=\dfrac{1}{2}AC，点P是直线MN上一动点，连接PD，PB，若BC=4，则如图，分别以线段AB的两个端点为圆心，以大于1/2AB长为 2012年9月24日如图所示，已知 ABC中，AB=AC，D是CB延长线上的一点，∠ADB=60度，E是AD上的一点，且有DE=DB,求证：AE=BE+BC不要用高线的方法，那个方法还木有学如图所示，已知 ABC中，AB=AC，D是CB延长线上的一点，∠ADB=60度，E是AD上的一点，且有DE=DB,求证：AE=BE+BC如图所示，已知 ABC中，AB=AC，D是CB延长线上的一点

(10分)如图,D是⊙O上一点,点C在直径BA的延长线上,且CD是⊙

E D C A 0 B 图1（1）证明：连接OD，如图所示：∵CD是⊙O的切线，∴OD⊥CD，∴∠ODE=90°，∵OE∥AD，∴∠BOE=∠OAD，∠ADO=∠DOE，∵OA=OD，∴∠ADO=∠OAD，∴∠BOE=∠DOE，在 OBE和 ODE中，OB =OD ∠BOE=∠DOE OEOE，∴ OBE≌ 2014年3月22日如图,CE是三角形ABC的外角角ACD的平分线,且CE交BA 75 d是三角形abc的边ba延长线一点，且ad=ba,e是ac一 10 D是 ABC的边BA延长线上的一点,AD=BA,E是边AC上 25 如图所示，在三角形ABC中，AB=AC，D是BA延已知如图D是三角形ABC的边BA延长线一点,有AD=BA,E是如图,已知Rt ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,BD的延长线与AE交于点F,求证:BF⊥AE 答案 [答案]见解析;[解析][分析]根据题意可以得到 ACE≌ BCD,然后根据全等三角形的性质和垂直的定义可以证明结论成立[详解]证明:∵ 如图，已知Rt ABC中，∠ACB=90°，CA=CB，D是AC上一点（1）如图1，点D是CA延长线上一点，点E在线段AB上，且AD=AE，连接BD和CE，延长CE交BD于点F，连接AF．求证：BD=CE；（2）在（1）得条件下，求∠AFD的度数；（3）如图2，点P是 ABC外一点，∠APB=45°，猜想PA、PB、PC三条线段长度之间在三角形ABC中，∠BAC=90°，AB=AC．（1）如图1，点D是

如图，已知点D为等腰直角 ABC内一点，∠ ACB=90°，∠ CAD

如图，已知点D为等腰直角$\triangle ABC$内一点，$\angle ACB={90}^{\circ }$，$\angle CAD=\angle CBD={15}^{\circ }$，E为AD延长线上一点，且CE=CA（1）求证：DE平分$\angle BDC$；（2）若点M在DE上，且DC=DM，求证：ME=BD已知:如图, ABC和 DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD,CE相交于点N,则下列五个结论:①AD=BE;②AP已知:如图, ABC和 DEC都是等边三角形,D是BC延长线上 2014年8月6日如图，在 ABC中，D是BC的中点，E是CA延长线上一点，DE交AB于F，且AE=AF。求证：EC=BF 我来答如图，在 ABC中，D是BC的中点，E是CA延长线上一点，DE 圆中的定理包括：1圆的定义：平面上所有到圆心距离相等的点构成的图形叫做圆。2圆的性质：（1）圆上任意两点之间的线段都是圆的直径。（2）圆的直径是圆上最长的线段，且等于圆的半径的两倍。如图,AB是⊙O的直径,弦CD⊥AB,E是CA延长线上的一点

如图，已知点D为等腰直角 ABC内一点，AC=BC，∠CAD

分析：在DE上截取DF=CD，先求出∠DAB=∠DBA=30°，根据等角对等边的性质可得AD=BD，再利用“边角边”证明 ACD和 BCD全等，根据全等三角形对应角相等可得∠ACD=∠BCD，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CDE=60°，从而判定出 CDF是等边三角形，再求出∠ECF=∠ACD=45°，利用“边角边 2016年5月18日如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且AB=AD=AO．（1）求证：BD是⊙O的切线；（2）若点E是劣弧BC上一点，AE与BC相交于点F，且 BEF的面积为8，cos∠BFA= 2 3 ，求 ACF的面积．如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且如图1所示，在Rt ABC中，∠C=90°，点D是线段CA延长线上一点，且AD=AB．点F是线段AB上一点，连接DF，以DF为斜边作等腰Rt DFE，连接EA，EA满足条件EA⊥AB．（1）若∠AEF=20°，∠ADE=50°，AC=2，求AB的长度；（2）求证：AE=AF+BC；（3）如图2，点F是线段BA延长线上一点，探究AE、AF、BC之间的数量关系，并证明．如图1所示，在Rt ABC中，∠C=90°，点D是线段CA延长线上 2014年12月29日已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且OA=AB=AD．（1）求证：BD是⊙O的切线；（2）若点E是劣弧BC上一点，AE与BC相交于点F，且BE=8，tan∠BFA=52，求⊙O的半径长．已知：如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上

如图，在 ABC中，AB=AC，D为CA延长线上一点，DF⊥BC于F，

2016年9月24日如图，在 ABC中，AB=AC，D为CA延长线上一点，DF⊥BC于F，交AB于E．求证： ADE是等腰三角形解答：证明：证法一：过点A作AG⊥BC于G，∵AB=AC，∴∠1=∠2，∵DF⊥BC，∴AG∥DF，∴∠1=∠AED，∠2=∠D，∴∠AED=∠D，如图，在Rt ABC中，∠ ACB=90°，AC=1，BC=7，点D是边CA延长线上的一点，AE⊥ BD，垂足为点E，AE的延长线交CA的平行线BF于点F，联结CE交AB于点G (3)当 BGE与 BAF相似时，求线段AF的长" /> 如图，在Rt ABC中，∠ ACB=90°，AC=1，BC=7，点D是边CA延长线上的一点，AE⊥ BD，垂足为点E，AE的延长线交CA的平行线BF于点F，联结CE交AB于点G (3)当 BGE与如图，在Rt ABC中，∠ ACB=90°，AC=1，BC=7，点D是边如图所示，在 ABC中，D是BC延长线上一点，CD=BC，E是CA延长线上一点，AE=2AC，若AD=BE，求证： ABC是直角三角形．答案分析由于告诉了AE=2AC，故延长AC至F，使CF=AC，连接BF，则 ADC≌ FBC，从而AD=BF，又AD=BE，从而BF=BE，即三角形BEF是等腰三角形，再根据AE=2AC，可得A是EF 如图所示，在 ABC中，D是BC延长线上一点，CD=BC，E 点评本题主要考查了全等三角形的判定与性质，等腰三角形“三线合一”的性质，难度中等．由题目条件“AE=2AC”联想到中线倍长是解答本题的关键．练习册系列答案如图所示在 ABC中D是BC延长线上一点CD=BCE是CA

如图1所示在Rt ABC中∠C=90°点D是线段CA延长线上一点

（3）如图2，过D作DM⊥AE交AE的延长线于M根据余角的定义和三角形的内角和得到∠2=∠B，证得 ADM≌ BAC，由全等三角形的性质得到BC=AM，由于EF=DE，∠DEF=90°，推出∠4=∠5，证得 MED≌ AFE，根据全等三角形的性质得到ME=AF，即可得到2015年4月20日平行线的性质 > 试题详情难度：使用次数：138 更新时间：纠错 1 如图， ABC中，AB=AC，D是CA延长线上的一点，且∠B=∠DAM．求证：AM∥BC．查看答案如图， ABC中，AB=AC，D是CA延长线上的一点，且∠B 如图，在Rt ABC中，∠ACB=90°，AC=1，BC=7，点D是边CA延长线的一点，AE⊥BD，垂足为点E，AE的延长线交CA的平行线BF于点F，连结CE交AB于点G．（1）当点E是BD的中点时，求tan∠AFB的值；如图在Rt ABC中∠ACB=90°AC=1BC=7点D是边CA延长

工作台生产线

连云港市凯源雷蒙磨公司

供应重钙磨粉机雷蒙机

矿山水资源检测费怎么账务处理

山东大理石浙江省开化县粉碎机

日产300吨金红石325目堇青石磨粉机出售

矿粉立式矿石磨粉机行情

钾长石矿的开采钾长石矿的开采钾长石矿的开采

新款旱采矿石立磨

制粉加工设备球磨机焙烧锂辉石磨粉机制粉加工设备球磨机焙烧锂辉石磨粉机制粉加工设备球磨机焙烧锂辉石磨粉机

每小时产600THPC石灰石粉碎

大型锰碳酸钙料研磨生产线全套设

磨灰机磨灰机磨灰机

矿山用方解石磨粉机多少钱

咸阳那有工业磨粉机厂家

HP943磨煤機規格

上海雷蒙机设计原理

中速磨有多少规格

福建三明市新建微粉磨

广州磨粉机有限公司

时产70吨雷蒙磨粉机器

立式磨高岭土磨粉机产量150TH

进料100的生石灰配多大雷蒙磨

plm矿石磨粉机型号意义

广西南宁石灰石多少

caf2颜色

方解石矿探矿证价格

14TPH石膏方解石磨粉机